THCon21 - Rsa Internal Attacker

Jun 17, 2021

3 mins read

Cryptography
Cryptography

Go back to write-ups list

Category: Cryptography

Creator: Nico

Description:

I’ve found this rsa implementation, it is quite strange. I have a public/private key and I’ve also intercepted a ciphertext but infortunately it was not for me, so I can’t read it. But I’am really curious, can you decrypt it ? :)

Attachments:

Analysing the script

The script attached to this challenge generates two prime numbers p and q, and the a modulus n = p*q. This modulus is common for both the users created afterwards.

p = getPrime(1024)
q = getPrime(1024)
n = p * q
e_a, d_a = new_user(p, q)
e_b, d_b = new_user(p, q)

Only e (and therefore d) is different for both users. So let’s do some quick maths. If we want to find our boss’ d from their e and n, we either need to find p and q, or φ. Here are the basic formulas linking them:

$$ \begin{cases} n = p \times q \\ \phi = (p - 1) \times (q - 1) \end{cases} $$

With some transformation, we can get rid of q and get an expression of p depending on n and φ.

$$ \phi = (p-1)\times(\frac{n}{p} - 1) \\ \Longleftrightarrow p\phi = (p-1)(n-p) \\ \Longleftrightarrow p^2 - (n+1)p + n - \phi = 0 $$

Well, we have a quadratic equation with p being an integer. This was a bit surprising, and I didn’t really know what to expect. Now let’s use one last formula : the formula that defines d

$$ e \times d = 1 \mod \phi $$

In other words, there exist a natural number k such as

$$ e \times d = k \times \phi + 1 $$

So now, if we bruteforce k, knowing our own e and d, we can find the φ, which was common to both my key and the boss’ key, and therefore p and q. And how do I know whether it’s the right φ or not? It’s the right φ if the solution p of the quadratic equation above using this φ is an integer!

Now let’s code the bruteforce script to find a φ that matches, using the info in output.txt:

from Crypto.Util.number import inverse, long_to_bytes

e1 = 0x8095
e2 = 0x22bb
d1 = 0x21a31ccbce8117f468e9c26e3a404659d585ea166606c85ff192466b8dd4d9650b110addef35e3effdf8cb8710235cf5843e688e977be0d32842e0b4fa493f451ad8d77d35672696cf4373eaa0c0093a6a0baa348f790fc466be559bd90e788505b795026df6e991f6e8769565e06f472a445676e2c99240eccab25cd44433e8a083e66912c7a81c81c190470188c699c1a24dac441956b46aa364623f2c78c4ffca49e89f8a6f6edc51140e744f80a968fa80901fc91b88d491829b334542fd3ef460ddfa9a729d981b0ae9fa12bd0901c919972020b5f9e661b34a914fff85732e45718a2d216018507e7406aed4543096df76ca6fcfa4ab5dd21a84f162fd
n = 0x8d926c44899930f8f3fc3ea04cb9dfa7eb309b6d8e932b531007c4d8479e1dd227365087feeced8f854b1b54cc947182ee2241fe526c758e630b44e0c196ce8dc0995124f94755b0601d3454f89f178db2ffb3adeafcac2f49b656aace2acdb63afcd62a8847aadc55ca2452dff8c65ea5bfcfe03411f3b63a2bc4b244126259e2e845c68f8c1cd2d275bd2e344d35da542503c72f153ded14f766efecdfc98605e6963c4b1a7197de9e56b4b61ca1ab648265e6775819935a005a089eff04c27083d385e8d73ebf56b47f875c5fa9984e026914e1cbfc02205e75d02dc0da392700b536bf0fc8decd043736441e69fecc696b2127589f2ac9700e30c4dc88ef
c = 0x2118ee5b546b529c6b8d8fba1638f046006d7de2c10571d179af958f65d223a9a78df91daa5913f39f97d47681e1e10b8c58b6b462caf1fd56c683129ea732927cf55a06441cde5b743d00582569c9bbf43dab3d7b46ddbf03b358ca6ee075bafcc06165efa8592474bf78732dec4433502579338f2b925a922e74704cf19f7dff414a451fbc24b4ace4a9d8a072fb4259ebc8452941eb9f100f1df0cf19d5718088867a17d52d1c3f1fd5f92c9b9c55cbe528fbfd130879c14bde651a9e402f50b851c753e5915882b02a1136b43e015c6d4fd07e48aa05be08e9faf533a763f21d29a9b7fe8f355a8ffcbf11dc96b1069df4e302a3b310ecf39f25300bb375

# Integer square root
def isqrt(x):
    if x < 0:
        raise ValueError('square root not defined for negative numbers')
    n = int(x)
    if n == 0:
        return 0
    a, b = divmod(n.bit_length(), 2)
    x = 2**(a+b)
    while True:
        y = (x + n//x)//2
        if y >= x:
            return x
        x = y

for k in range(1, 10000):
    phi = (e1*d1 - 1) // k
    
    possible_p = (isqrt(n*n - 2*n*(phi+1) + (phi-1)**2) + n - phi + 1)//2

    if possible_p > 0 and n % possible_p == 0:
        p = possible_p
        q = n // possible_p
        d_boss = inverse(e2, phi)
        print(f"k: {k}, p: {p}")
        print("Boss d:", d_boss)
        print("Message:", long_to_bytes(pow(c, d_boss, n)))
        break

Note: I used a square root function because the solution of the quadratic equations has a square root in it. The isqrt function is a function to approximate the square root to an integer, because Python wouldn’t compute the square root of very big integers.

This gives us the following result:

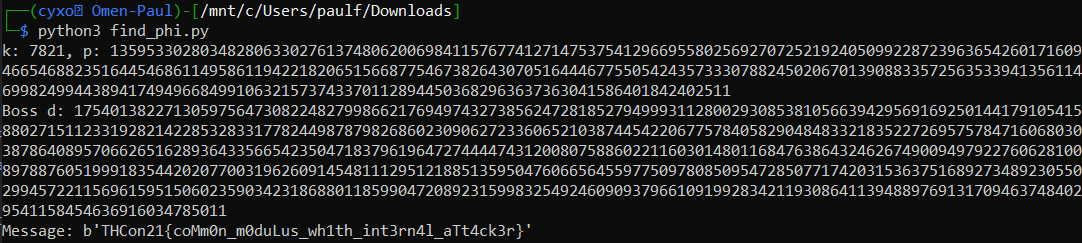
Challenge solution

The flag mentions “common modulus”. The method I used in this challenge might not be the usual one for common modulus challenges (as far as I remember, I solved common modulus challenges in the past, and I don’t recall using a weird square root function), but the maths are correct so it solves the problem anyway 🤷‍♂️

Go back to write-ups list

Sharing is caring!